nserman@fsb.hr Transfer Function Concept Digest
8. RELATIONSHIP BETWEEN BLOCKS STABILITY AND STABILITY OF THE SYSTEM AS A WHOLE
Let us present the transfer function in general as a ratio of the numerator and the denominator:
![]()
In the chapter 5. it has been shown that the system described by G(s) is stable if there is no pole at the right-hand side of the complex plane. In that case the transients of the systems response to any kind of perturbation vanish in time. Any pole located at the right-hand side would make the transients diverge towards infinity, i.e. to the limit of the system linearity.
By expressing the block transfer functions HA and HB in terms of numerator and denominator system transfer functions in various interactions look as follows:
For blocks in series:
![]()
For blocks in parallel:
![]()
For blocks in negative feedback closed loop:
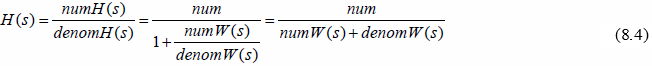
The numerator in 8.4 is denoted by num. Its form would depend on the output variable taken. However, as numerator as such is irrelevant to the system stability it exact form is not considered in this context.
Equations (8.2) and (8.3) present open-loop systems. It is a common name for systems consist of exclusively serial and parallel connections. Their transfer function denominator equals a product of the blocks denominators. Therefore the whole system transfer function poles are identical to the poles of the blocks involved. If the blocks are stable, all their poles are located at the left-hand side of the complex plane hence the system as a whole is stable as well.
Conclusion: Any open-loop system as a whole is stable if all its components are stable.
As for closed-loop system it is not that straight forward. As per (8.4) the closed loop transfer function denominator is a sum of the numerator and the denominator of the same loop open-loop transfer function. Consequently, the poles of a closed-loop transfer functions are not the same as the poles of the same loop open- loop transfer function. Hence all possibilities are open:
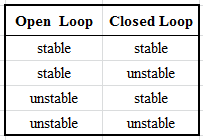
Conclusion: There is no straight relationship between closed loop stability system and stability of its components.
Obviously, the stability of a closed-loop system is not determined by the open-loop dynamics itself. This rises a question – are there some dynamic properties of the open-loop system that can ensure the closed-loop stability. The answer is given by the Nyquist stability criterion. It enables us to tackle a closed-loop stability problem even without a full knowledge on the exact open-loop dynamics.