nserman@fsb.hr Transfer Function Concept Digest
9. NYQUIST STABILITY CRITERION
Closed-loop system is stable if all the transients are vanishing in time. They are supposed to vanish regardless of how the system is disturbed. It is irrelevant which variable is monitored as all the transients are supposed to vanish.
Therefore, closed-loop system structure can be presented by fig 9.1.
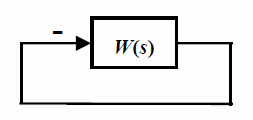
Fig. 9.1 Negative feedback closed-loop system presented from the stability point of view.
Nyquist stability criterion in its very simplified form can be formulated as follows:
Closed-loop system made up of a stable open-loop W(s) that is enclosed by a negative feedback is stable if the open-loop frequency response W(jω) in Nyquist diagram does not encircle the point [ -1, j0 ] in Cartesian coordinates, that is [ modulus=1, arg = -180° ] in polar coordinates.
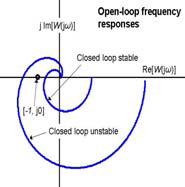
Fig. 9.2 Simplified presentation of the Nyquist stability criterion in Nyquist diagram.
Two different open-loop frequency responses are presented In fig. 9.2.
One of them encircles the point [ -1, j0 ]. According to Nyquist stability criterion the closed loop containing the W(s) with such a frequency response is unstable.
The other one does not encircle the point [ -1, j0 ]. It intersects the real axis somewhere between its origin and the point [ -1, j0 ]. According to Nyquist stability criterion the closed loop containing the W(s) with such a frequency response is stable.
The same open-loop frequency responses from fig. 9.2 are presented in Bode diagram in fig. 9.3. The point [ -1, j0 ] that is a single point in Nyquist diagram maps into two points in the Bode diagram. One of them is in the phase part of the diagram and the other is in the amplitude part. The phase-frequency characteristic intersection with φ = -180° line determines the critical frequency ωcrit = ω(φ = -180°) for a given open-loop dynamics W(s).
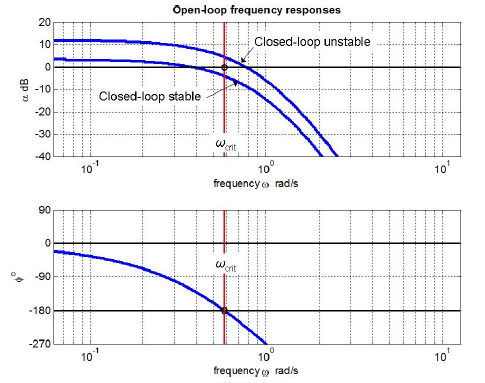
Fig. 9.3 Nyquist stability criterion presented in Bode diagram.
The closed-loop stability depends on W(s) dynamic gain at the critical frequency ωcrit. If the gain α(ωcrit) is less than unity, i.e. when αdB(ωcrit) < 0, the closed loop is stable, otherwise the same is unstable.
Nyquist criterion presentation in Bode diagram is in the core of closed loop dynamics qualitative analysis detailed in Chapter 11.



