Nikola Šerman, prof. emeritus Linear Theory
nserman@fsb.hr Transfer Function Concept Digest
5. SOLUTION OF LINEAR DIFFERENTIAL EQUATION WITH CONSTANT COEFFICIENTS
Solution of a linear differential equation with constant coefficients (2.1) describes the change of the output y(t) for a given change of input x(t) at given initial conditions (2.2) and (2.3).
It is made in two parts:
![]()
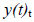 part is called transients. It consists of a sum of exponential functions:
part is called transients. It consists of a sum of exponential functions:

where:
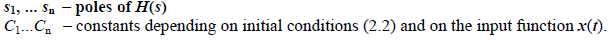
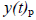 part is called particular solution – it satisfies the equation (2.1) particularly for a given x(t).
part is called particular solution – it satisfies the equation (2.1) particularly for a given x(t).
Transients are always present in the solution of the equation (2.1), regardless of how the system described by the equation(2.1) is perturbed. It can be perturbed by either:
- non-zero x(t);
- non-zero initial conditions (2.2);
- both of them.
There is a case when all the initial conditions (2.2) are equal zero, plus x(t)=0, plus all the constants C in (5.2) are equal zero as well as the particular integral ![]() = 0. In that case the system is initially in equilibrium. Its state is not disturbed by any outer influence, so the solution of (2.1) becomes y(t) = 0.
= 0. In that case the system is initially in equilibrium. Its state is not disturbed by any outer influence, so the solution of (2.1) becomes y(t) = 0.
If root si is a real number (si = σ0) than the corresponding summand in the transients (5.2) is a monotonic exponential function:
![]()
Denominator in (4.3) is an n-th order polynomial, so depending of the polynomial’s coefficients some of its roots can be complex numbers. In real-world systems all the polynomial’s coefficients are real numbers. In such a case the complex roots are coming up in conjugate pairs.
For a conjugate complex pair ![]() and
and ![]() an oscillatory function appears in the solution as a summand:
an oscillatory function appears in the solution as a summand:
![]()
The exponential term in both (5.3) and (5.4) rises a question of transients convergence, i.e. the question of stability.
System is stable if the transients converge to zero in time. For that to happen the real parts of all the poles in the system’s transfer function MUST be negative, i.e. no pole is located at the right side of the complex plane.
Hence the transfer function concept makes possible examining complex systems stability without figuring out the exact solution for the poles themselves.



