Nikola Šerman, prof. emeritus                                                                                  Linear Theory
nserman@fsb.hr                                                                                                         Transfer Function Concept Digest

4. TRANSFER FUNCTION

According to (3.5), function f(t) n-th derivative L-transform generally depends on the function itself as well as on its initial conditions.

When initial conditions are equal to zero, i.e. when it holds:

Function f(t) n-th derivative L-transform becomes an algebraic product of F(s) and the n-th power of s:

In the time domain relationship between output and input is defined by a differential equation (2.1) . However, when moved to the frequency domain by (4.2) the same relationship takes a simple algebraic fraction form.  This form is called transfer function.

It can be expressed as:

either

as a fraction of polynomials with rising powers of s :

where:

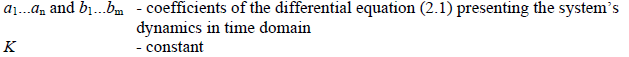
or

by means of poles s₁….s_m (roots of the denominator) and zeros s₁….s_n (roots of the nominator) of the transfer function H(s):

Due to the transfer function definition (4.3) or (4.4), the output Y(s) L-transform can be obtained by a simple multiplication of the transfer function H(s) with the input X(s) L-transform:

This simple frequency domain algebraic relationship between input, output and the transfer function makes the transfer function concept such a powerful tool in dealing with complex linear dynamic systems.