Nikola Šerman, prof. emeritus Linear Theory
nserman@fsb.hr Transfer Function Concept Digest
3. LAPLACE TRANSFORMATION (L-TRANSFORM)
By Laplace transformation a function of time f(t) is mapped into function F(s), where s is a complex variable.
The transformation is performed by solving the following integral:

where:
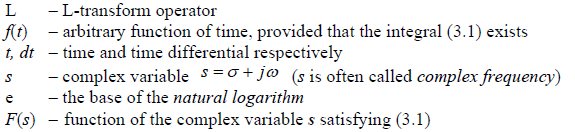
The transformation is possible when the following two conditions are met:
- f(t) = 0 for t < 0
- f(t) belongs to the class of exponential order functions, i.e. when the integral
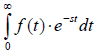 exists.
exists.
Though f(t) and its transform F(s) have generally very different forms, they are usually considered as two appearances of a single entity – f(t) in the time domain and F(s) in the frequency domain. In the table 3.1 there are time domain and frequency domain presentations of some functions used in dealing with dynamic systems evaluation.
Complex numbers
For a given complex value of s, corresponding value of F(s) is a complex number. Any complex number z can be analytically presented in two forms:
![]()
Where:
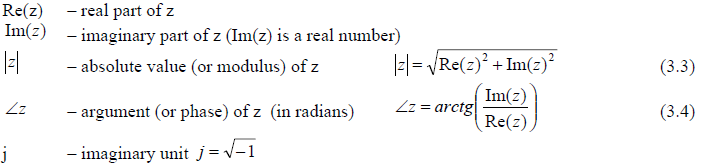
Geometrically, complex number z is a point in the complex plane, where Re(z) and Im(z) present Cartesian coordinates and ![]() and
and ![]() present polar coordinates of the point z.
present polar coordinates of the point z.
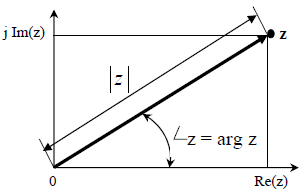
Fig. 3.1 Complex number z in a complex plane
![]()
L-transform of the function derivatives
For the 1st derivative of function f(t) it holds:
![]()
By recursive use of (3.5), L-transform of the n-th order derivative of function f(t) can be obtained as:
![]()
An assumption of all the initial conditions being equal zero are taken for the further paragraphs.
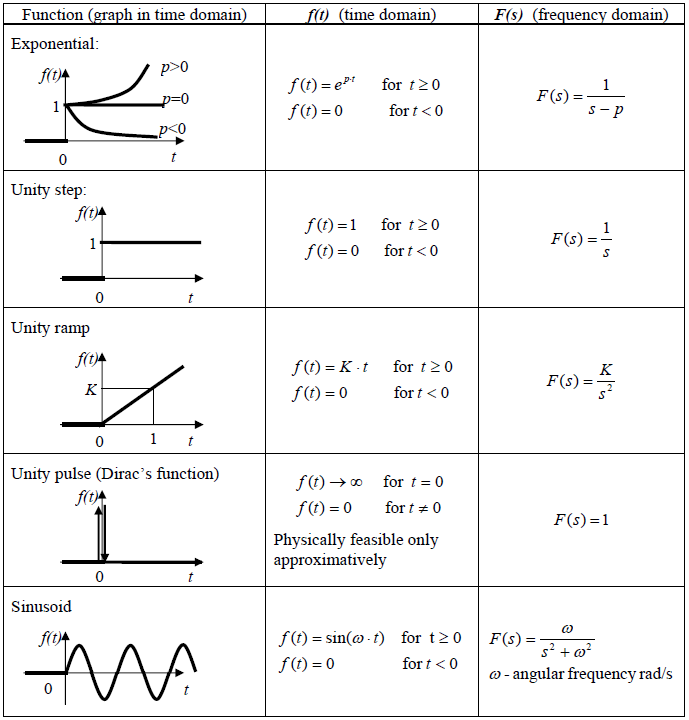
Table 3.1. Some characteristic functions presented in both the time and the frequency domain



