nserman@fsb.hr Transfer Function Concept Digest
10. ELEMENTARY BLOCKS
10.5 First Order Lead
When the zero of the transfer function (10.3) is a real negative number z = – ω0 and constant K equals ω0, the transfer function becomes:
![]()
In control engineering this elementary block is often named first-order lead. Its only parameter denoted by T is referred to as time constant , where ![]() .
.
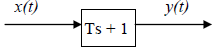
Fig 10.17 Block presentation of the first-order lead
The first-order lead can be interpreted as a parallel connection of a differentiator and the unity gain as its shown in fig. 10.18.
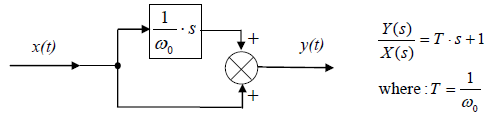
Fig 10.18 First-order lead structure
First-order lead step response is shown in fig. 10.19
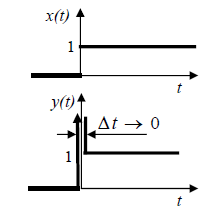
Fig 10.19 First order lead step response – sum of Dirac’s δ function and unity step.
First-order lead frequency response in Nyquist diagram is shown in fig. 10.20.
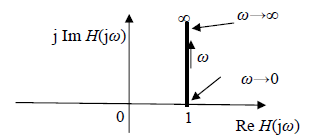
Fig 10.20 First-order lead frequency response in Nyquist diagram.
First-order lead frequency response in Bode diagram is shown in fig. 10.21
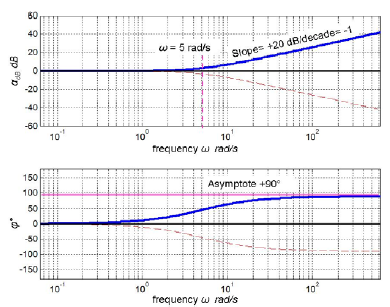
Fig 10.21 First-order lead frequency response with T = 0.2 s in Bode diagram. Dashed lines present the respective characteristics of the first-order lag which confirm their mutual symmetry as expected.




