nserman@fsb.hr Transfer Function Concept Digest
10. ELEMENTARY BLOCKS
10.4 Differentiatior
When the zero of the transfer function (10.3) equals zero, i.e. for z = 0, it makes the transfer function of differentiator. Differentiator is presented as a block in fig 10.14. Though it is not physically feasible as an autonomous component, it is often used in combination with first-order lag.
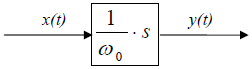
Fig. 10.14 Block presentation of a differentiator
In the time domain differentiator is defined by the following differential equation.
![]()
Its transfer function is.
![]()
where ω0 is a constant with dimension of angular frequency rad/s.
Due to the fact that unity step function presents the discontinuity at t = 0, the unity step response of differentiator could be imagined as Dirac’s function δ(t), i.e. as an infinite pulse of a zero duration:
![]()
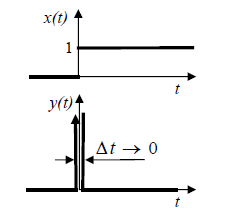
Fig 10.14 Step response of differentiator – Dirac’s δ function.
Frequency response of differentiator coincides with positive part of imaginary axis in Nyquist diagram, so φ = +90° regardless to the value of ω0, as is shown in fig. 10.15.
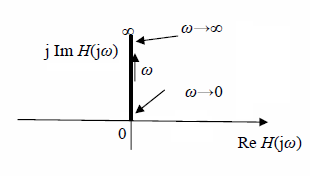
Fig 10.15 Differentiator frequency response in Nyquist diagram.
Differentiator frequency response in Bode diagram is shown in fig. 10.16.
Amplitude-frequency characteristic is a straight line with a slope of +20 dB/decade, which is referred to as positive unity slope (or slope = +1). Dynamic gain lines cross the unity gain axis (αdB = 0) at frequency ω0.
Phase-frequency characteristic is a horizontal straight line at φ = +90° regardless of the ω0 value.
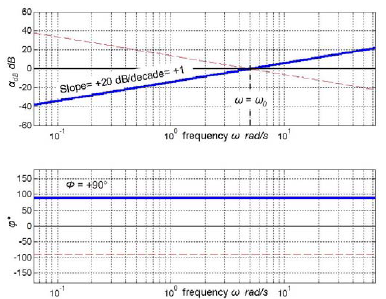
Fig 10.16 Differentiator frequency response in Bode diagram for ω0 = 5 rad/s (solid lines). Thin dashed line presents the characteristics of an integrator.
Differentiator frequency characteristics in Bode diagram are the mirror images of respective integrator characteristics. It is due to the fact that their transfer functions are mutually reciprocal. The same effect will be demonstrated on the first-order lead block with respect to the first-order lag.




